Framing and windowing¶

Contents

Frames extraction
Windows functions

Frames extraction ¶

Provides the Frames class to extract frames from raw signals

Extracts overlapping frames from raw (sampled) signals:

array ---> Frames ---> array

Examples

>>> import numpy as np
>>> from shennong.frames import Frames

Build a discrete signal

>>> a = np.arange(10)
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

Computes frames of 3s with a shift of 1s (here we assume fs=1Hz for simplicity)

>>> f = Frames(sample_rate=1, frame_shift=1, frame_length=3)
>>> b = f.make_frames(a)
>>> b
array([[0, 1, 2],
       [1, 2, 3],
       [2, 3, 4],
       [3, 4, 5],
       [4, 5, 6],
       [5, 6, 7],
       [6, 7, 8],
       [7, 8, 9]])

class shennong.frames.Frames(sample_rate=16000, frame_shift=0.01, frame_length=0.025, snip_edges=True)[source]¶

Bases: shennong.base.BaseProcessor

Extract frames from raw signals

property sample_rate¶

Waveform sample frequency in Hertz

Must match the sample rate of the signal specified in process

property frame_shift¶: Frame shift in seconds

property frame_length¶: Frame length in seconds

property snip_edges¶

If true, output only frames that completely fit in the file

When True the number of frames depends on the frame_length. If False, the number of frames depends only on the frame_shift, and we reflect the data at the ends.

property samples_per_frame¶: The number of samples in one frame

property samples_per_shift¶: The number of samples between two shifts

get_params(deep=True)¶

Get parameters for this processor.

Parameters: deep (boolean, optional) – If True, will return the parameters for this processor and contained subobjects that are processors. Default to True.
Returns: params (mapping of string to any) – Parameter names mapped to their values.

property log¶: Processor logger

abstract property name¶: Processor name

nframes(nsamples)[source]¶

Returns the number of frames extracted from nsamples

This function returns the number of frames that we can extract from a wave file with the given number of samples in it (assumed to have the same sampling rate as specified in init).

Parameters: nsamples (int) – The number of samples in the input
Returns: nframes (int) – The number of frames extracted from nsamples
Raises: ValueError – If samples_per_shift == 0, meaning the sample rate is to low w.r.t the frame shift.

set_logger(level, formatter='%(levelname)s - %(name)s - %(message)s')¶

Change level and/or format of the processor’s logger

Parameters

level (str) – The minimum log level handled by the logger (any message above this level will be ignored). Must be ‘debug’, ‘info’, ‘warning’ or ‘error’.
formatter (str, optional) – A string to format the log messages, see https://docs.python.org/3/library/logging.html#formatter-objects. By default display level and message. Use ‘%(asctime)s - %(levelname)s - %(name)s - %(message)s’ to display time, level, name and message.

set_params(**params)¶

Set the parameters of this processor.

Returns: self
Raises: ValueError – If any given parameter in params is invalid for the processor.

first_sample_of_frame(frame)[source]¶: Returns the index of the first sample of frame indexed frame

last_sample_of_frame(frame)[source]¶: Returns the index+1 of the last sample of frame indexed frame

times(nsamples)[source]¶

Returns an array of (tstart, tstop) times of each frames of a signal

Parameters: nsamples (int) – The number of frames of the considered signal
Returns: times (array, shape = [nframes, 2]) – The start and stop times of each frame extracted from nsamples samples.

boundaries(nframes)[source]¶

Returns an array of (istart, istop) index boundaries of frames

Parameters: nframes (int) – The number of frames to generate
Returns: boundaries (array, shape = [nframes, 2]) – The start and stop indices of each frame extracted from nsamples samples.

make_frames(array, writeable=False)[source]¶

Returns an array divided in frames

Parameters

array (array, shape = [x, ..]) – The array to be divided in frames
writeable (bool, optional) – Default to False. When True, the returned array is writable but the frames are made of copies of the original array. When False, the result is read-only but this optimizes the process: no explicit copy is made of the orignal array, only views are used. (see https://docs.scipy.org/doc/numpy-1.15.0/reference/generated/ numpy.lib.stride_tricks.as_strided.html)

Returns

frames (array, shape = [nframes(x), samples_per_frame, …]) – The frames computed from the original array

Windows functions ¶

Implementation of different types of window functions

This is usefull when computing frames for features extraction. Uses the kaldi implementation.

The implemented window functions 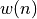$w(n)$ are, with length noted $N$ :

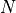rectangular:

$w(n) = 1$
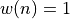
hanning:

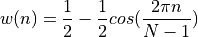
$w(n) = \frac{1}{2} - \frac{1}{2} cos(\frac{2\pi n}{N-1})$
hamming:

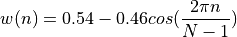
$w(n) = 0.54 - 0.46 cos(\frac{2\pi n}{N-1})$
povey (like hamming but goes to zero at edges):

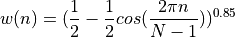
$w(n) = (\frac{1}{2} - \frac{1}{2} cos(\frac{2\pi n}{N-1}))^{0.85}$
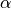blackman, with blackman_coeff noted as $\alpha$ :

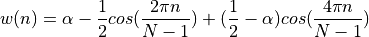
$w(n) = \alpha - \frac{1}{2} cos(\frac{2\pi n}{N-1}) + (\frac{1}{2} - \alpha) cos(\frac{4\pi n}{N-1})$

Examples

>>> from shennong.window import window
>>> window(5, type='hamming')
array([0.08, 0.54, 1.  , 0.54, 0.08], dtype=float32)
>>> window(5, type='rectangular')
array([1., 1., 1., 1., 1.], dtype=float32)
>>> window(5, type='povey').tolist()
[0.0, 0.5547847151756287, 1.0, 0.5547847151756287, 0.0]

shennong.window.types()[source]¶: Returns the supported window functions as a list

shennong.window.window(length, type='povey', blackman_coeff=0.42)[source]¶

Returns a window of the given type and length

Parameters

length (int) – The size of the window, in number of samples
type ({'povey', 'hanning', 'hamming', 'rectangular', 'blackman'}) – The type of the window, default is ‘povey’ (like hamming but goes to zero at edges)
blackman_coeff (float, optional) – The constant coefficient for generalized Blackman window, used only when type is ‘blackman’

Returns

window (array, shape = [length, 1]) – The window with the given type and length

Raises

ValueError – If the type is not valid or length <= 1

Framing and windowing¶

Frames extraction¶

Windows functions¶

Frames extraction ¶

Windows functions ¶